In the previous blog, we talked about setting up our pull chain for the parts that support the top 80% of the products you sell to customers. We discussed understanding the pull chain for each type of part that goes into your finished product. Next, we need to consider the customer demand for the products that make up your top 80% of sales.
Let’s say that our pull chain for the parts we want to look at looks like this:

Assuming that we want to keep two day’s worth of material at the assembly location, four days of material in the supermarket, and our supplier takes 20 days to replenish an order, how much material do we need at each location?
To calculate an aggregate quantity for the piece parts that support the finished unit demand (the parent), the formula for the pull quantity is:
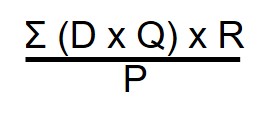
Let’s look at each of the items in the formula. The D is the demand of the parent the parts go into. Q is the quantity of this part that the parent consumes R is the replenishment time, or how long it takes to replenish a pull quantity when it is empty. P is package size. If the part comes in a plastic bag that contains fifty pieces that is the package size. The default quantity in this formula is one.
Calculate the bin quantity for each location. To set up our pull system, we’ll use a two-bin system. Imagine two bins each with the same part and quantity in them. When the first bin goes empty are we out of parts?
No, because we have a second bin full of parts. The formula calculates how many parts we need to keep in the two bins based upon the replenishment time. It is important to realize you have to put the aggregate parent demand into daily demand since we are calculating pull quantities based upon how many days of material we need. Look at the table below for part ABC.
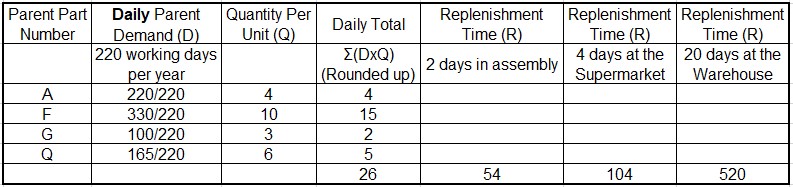
We can see that this part is used in parents A, F, G, and Q. Each of those parents’ demand is shown divided by the number of working days to calculate a daily quantity D. In this example we build 250 units a year and there are 250 working days. Our D quantity in this example would be one.
This is multiplied by how many are used on each parent which is Q. Round this quantity to the next highest whole number. It’s impossible to have ½ of a part. Just so you are aware, these two numbers D and Q should stay static.
Now, all we have to do is multiply ∑(D x Q) by the replenishment time R. This number varies depending upon how much material we want to carry at each location. Continuing this process with the rest of the parents F, G and Q we see that we need to carry 52 parts to support two days of replenishment time in assembly.
This is two containers each with 26 parts in them for a total of 52 parts. The Supermarket quantity is 104 since we are carrying 4 days of material- 4 x 26. This means each container in the warehouse has 52 pieces in them.
The warehouse quantity if the only one we can’t control. We need two containers each with 520 pieces in them since it takes the supplier twenty days to replenish an order. If we only kept 20 days total, then after day 10 the first bin would go empty and go the supplier and they would take 20 days to respond. That would not be good.
Something to consider, while it sounds like you have 40 days of material in the warehouse, realize most of the time only the second container is full. The first container is being emptied on a daily basis. On average, there will be one container’s worth of material in the system. This is how you can get to 12 or more turns easily and quickly. This will have a dramatic positive impact on your cash flow!
Next week we will finish our pull discussion by covering the pull cards that we will want to use to support the system.
As always, it is an honor to serve you and I hope that you and your company are getting better every day!
Follow me on Twitter
Join me on LinkedIn
Listen to the podcast here
